ソートアルゴリズムを真面目に実装する(応用情報技術者試験)
タイトルの通り、ソートアルゴリズムを真面目に実装します。 言語はPython、実装するソートアルゴリズムはクイックソート・ヒープソート・マージソートです。
ソートは基本的に標準ライブラリのsort関数に投げがちなので、内部がどうなっているかを気にすることがないかと思います。
今回は応用情報技術者試験の対策も兼ねて、真面目にソートを実装します。
なお、めんどくさいので昇順ソートしか実装しません()
参考文献
- 応用情報技術者試験合格教本(技術評論社)
- プログラミングコンテストのためのアルゴリズムとデータ構造(マイナビ出版)
- クイックソート
- ヒープソート
- マージソート(Qiita)
- マージソート
クイックソート
クイックソートは、分割統治の考え方でソートを行うアルゴリズムです。
下記のような配列を考えたとき、その配列に対してpivotと呼ばれる軸を設定し、そのpivot未満の配列とpivot以上の配列に分割していきます。
これを再帰的に繰り返すことで、整列済みの配列を得るアルゴリズムです。また、安定なソートではありません。
計算量
平均計算量は、O(NlogN)となります。
具体的な計算量の導出はこちらが参考になりました。
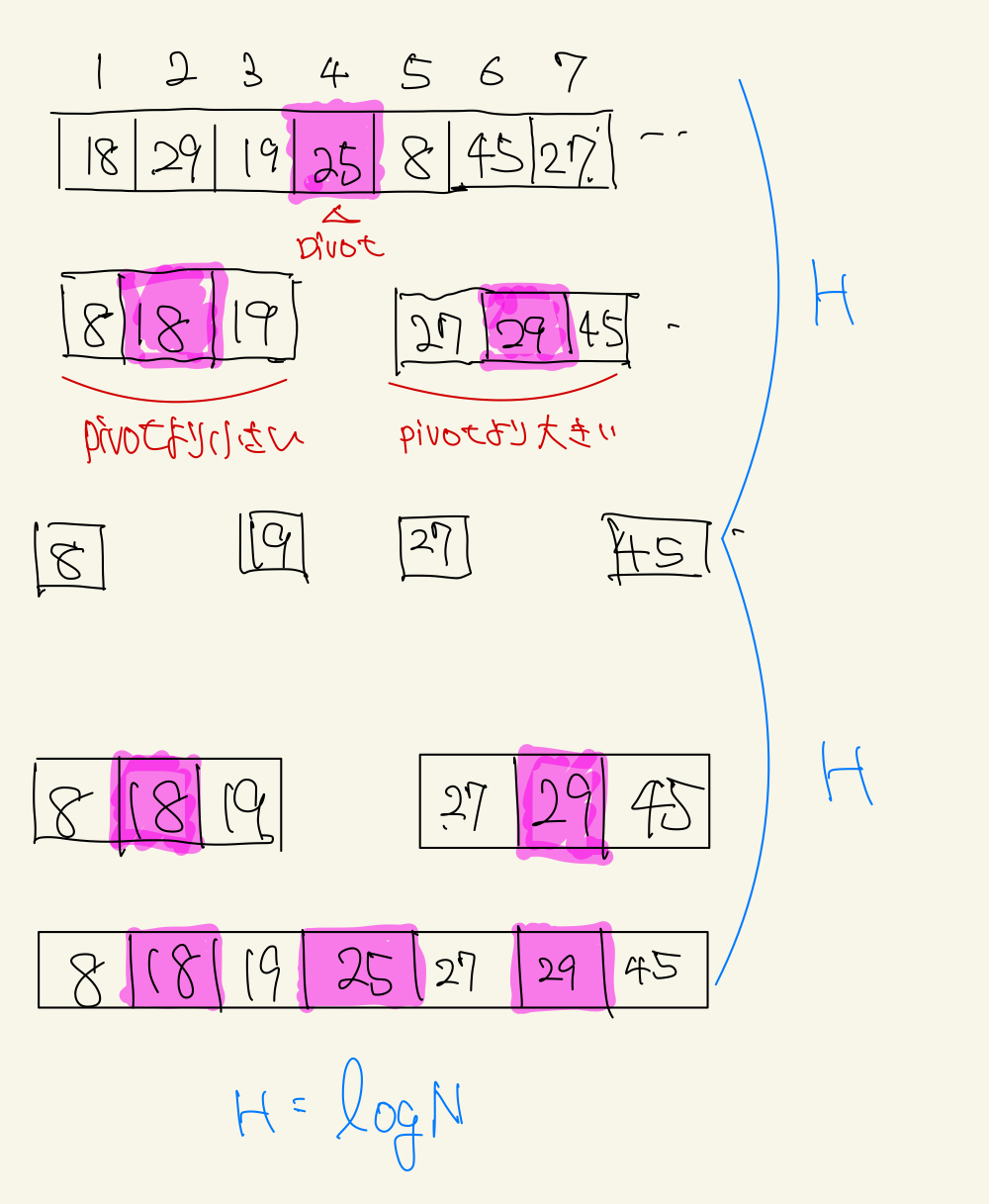
ざっくり言えば、適切にpivotを選んだ場合上記の画像で示す通りpivotによる分割と結合はそれぞれ回数H = logNで抑えることができます。
それぞれの高さに関して、N回比較が発生するので、計算量はO(NlogN)であるとわかります。
最悪計算量
ただし、予めソートされたデータに対して最大値/最小値をpivotとして取り続けた場合は最悪計算量がO(N^2)となります。
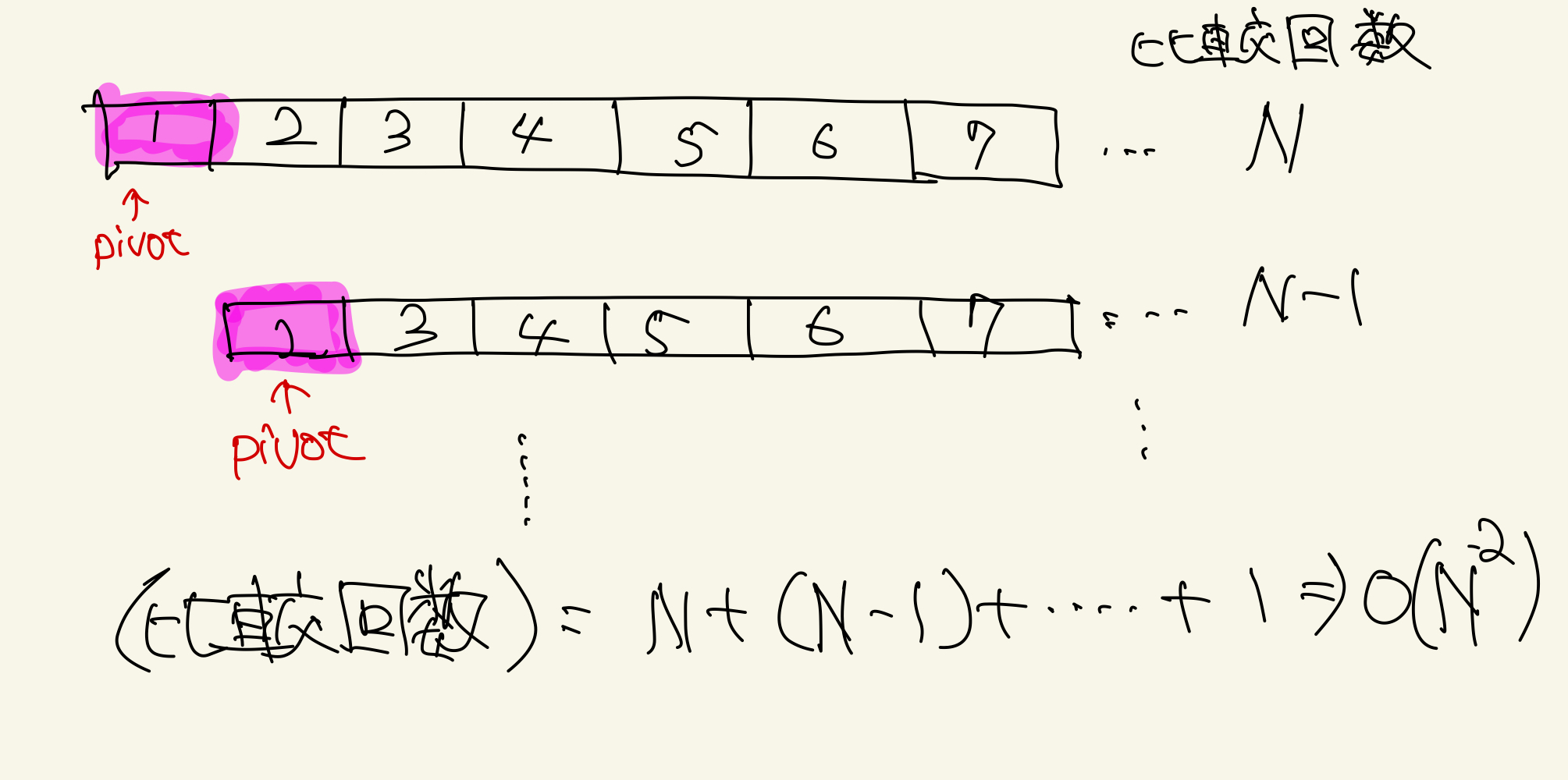
実装
A = list(map(int, input().split()))
l = 0
r = len(A) - 1
def quick_sort(tgt):
tgt_len = len(tgt)
if len(tgt) <= 1:
return tgt
pivot = tgt[0]
left = []
right = []
for i in range(1, tgt_len):
if tgt[i] <= pivot:
left.append(tgt[i])
else:
right.append(tgt[i])
return quick_sort(left) + [pivot] + quick_sort(right)
res = quick_sort(A)
print(res)
ヒープソート
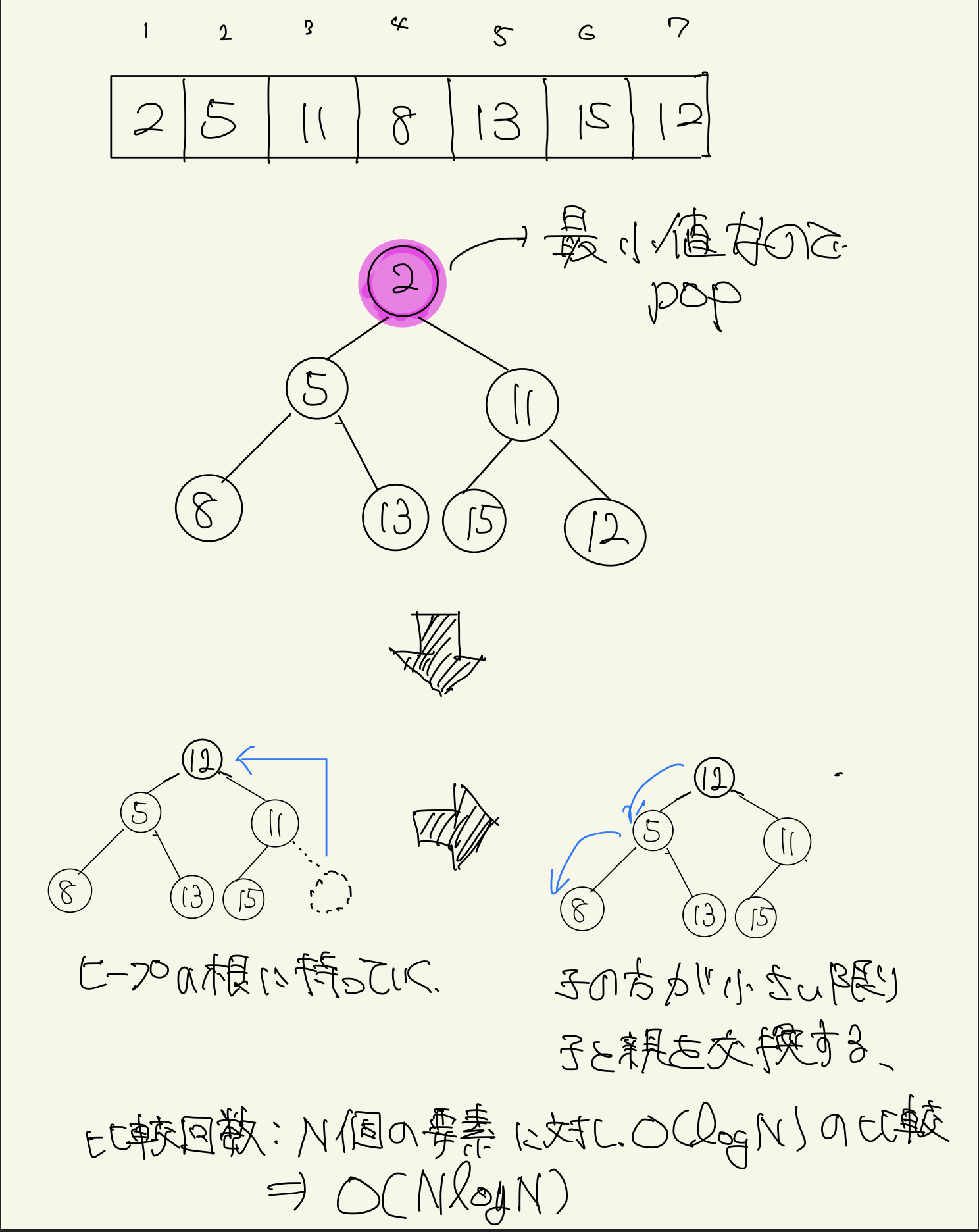
ヒープソートはヒープの再構成がO(logN)でできることを利用したソートアルゴリズムです。
ヒープの根が常に配列の最小値となっているので、ヒープの根をpop→ヒープを再構築...を繰り返し、popした順に配列を作ればO(NlogN)でソートできます。
ヒープに突っ込むため、安定なソートではないですが、常に計算量がO(NlogN)となります。
実装
ヒープを自力で実装し、ヒープからどんどんpopしていく方針を取ります。
class Heap:
def __init__(self, arr:list):
self.arr = []
for item in arr:
self.push(item)
def push(self, x):
self.arr.append(x)
child = len(self.arr) - 1
while child > 0:
parent = (child - 1)//2
if self.arr[parent] < x:
break
else:
self.arr[child] = self.arr[parent]
child = parent
self.arr[child] = x
def root(self):
return self.arr[0] if self.arr else None
def pop(self):
if not self.arr:
return None
root = self.arr[0]
self.arr[0] = self.arr[-1]
self.arr.pop()
parent = 0
smallest_index = parent
heap_size = len(self.arr)
while 2*parent+1 < heap_size:
l = 2*parent+1 # 左の子
r = l+1 # 右の子
# 自分、左の子、右の子の中で、最小のものを選び取る
if (r < heap_size) and (self.arr[parent] >= self.arr[r]):
smallest_index = r
if (l < heap_size) and (self.arr[smallest_index] > self.arr[l]):
smallest_index = l
# 自分が最小になった時点で、ヒープ化されたのでbreak
if smallest_index == parent:
break
# 親と子を入れ替える
self.arr[parent], self.arr[smallest_index] = self.arr[smallest_index], self.arr[parent]
parent = smallest_index
return root
def heap_sort(arr):
heap = Heap(arr)
N = len(arr)
print(heap.arr)
result = []
for _ in range(N):
result.append(heap.pop())
print(heap.arr)
return result
if __name__ == "__main__":
sample = [1, 1, 2, -1, 100, 92]
result = heap_sort(sample)
print(result) # -> [-1, 1, 1, 2, 92, 100]
マージソート
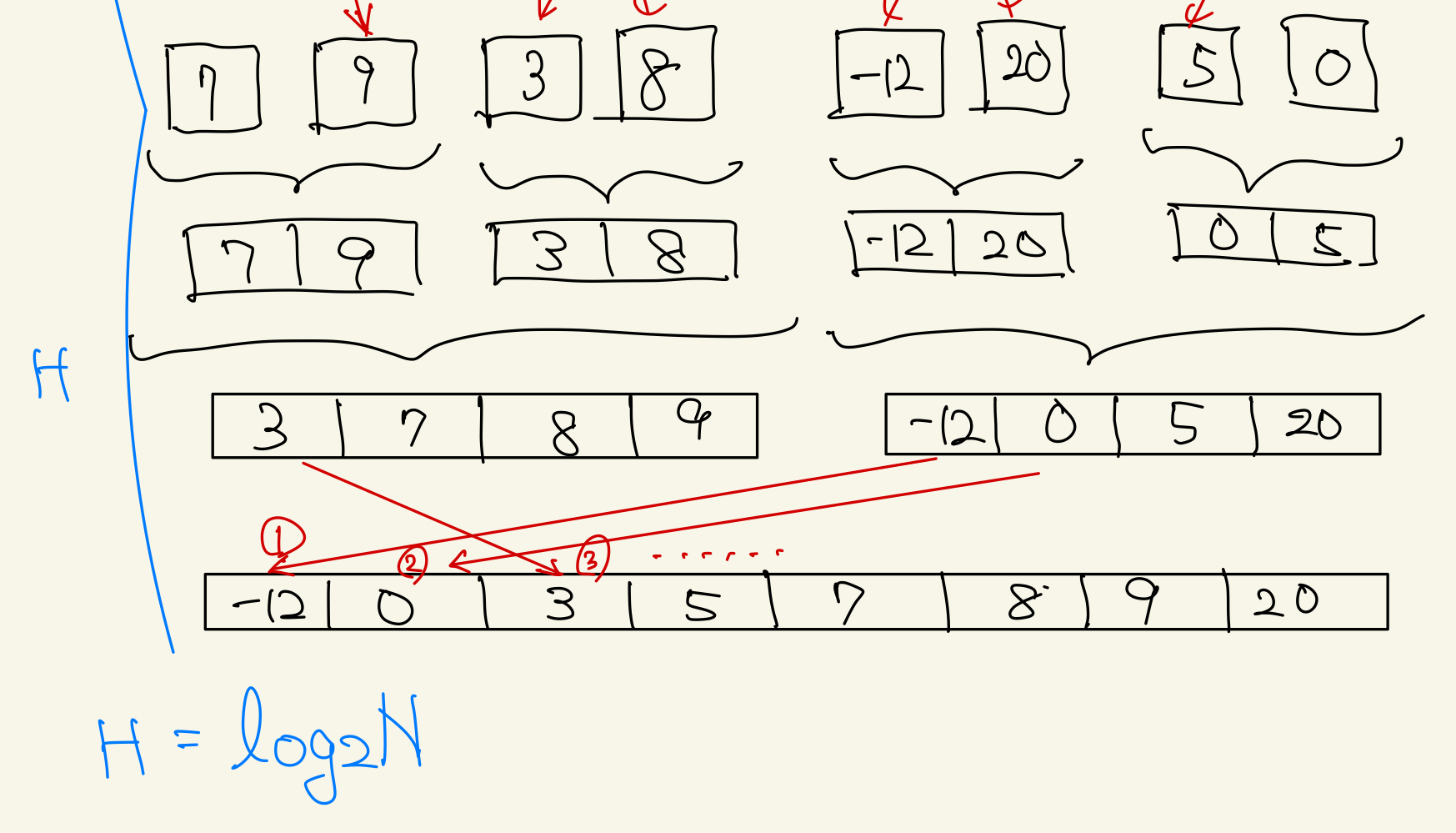
マージソートも、分割統治法の考え方を用いてソートを行うアルゴリズムです。 下記画像のように、まず要素が一つになるまで分割を繰り返します。
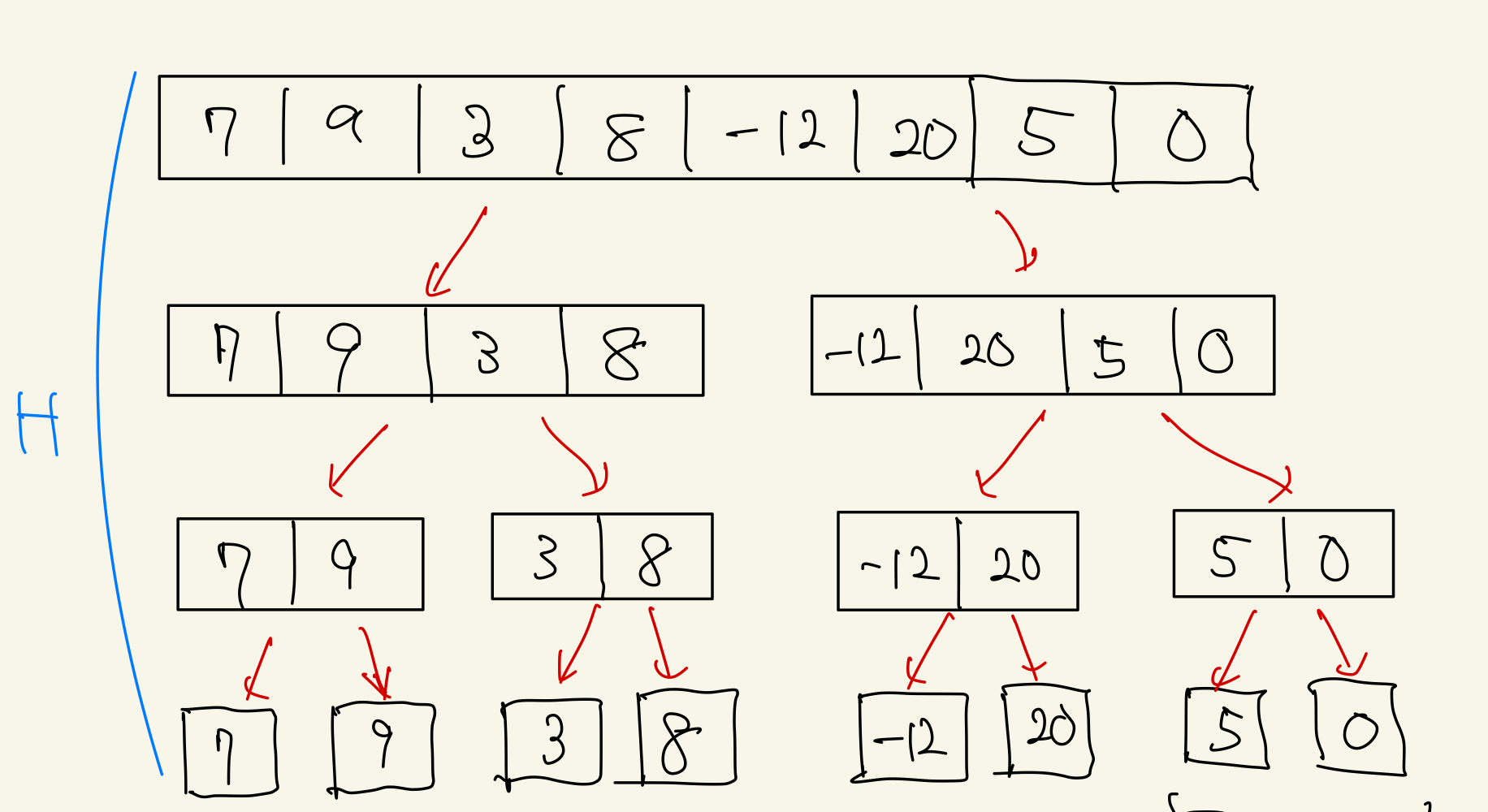
その後、分割した配列を2つずつマージしていきます。 このとき、分割した配列を結合する際に、昇順になるように入れていきます。各配列はソート済みであるので、それぞれ先頭のindexから順に比較していけば良いことになります。
計算量
こちらの説明がとてもわかりやすいです。
上の図で示した通り、分割とマージのプロセスはそれぞれH = logNで抑えられます。
マージの際には、それぞれの分割のレイヤーでN回比較が走るので、結果的に計算量はO(2NlogN) = O(NlogN)となります。
実装
再帰的な実装を行います。(実は分割のところがO(N)かかっているのではないかという説があります)
def merge_sort(data):
if len(data) <= 1: return data
mid = len(data) // 2
# 再帰的に分割していく
left = merge_sort(data[:mid:])
right = merge_sort(data[mid::])
return merge(left, right)
def merge(left, right):
result = []
i, j = 0, 0
# 配列の先頭が最小値になっているので、毎回比べながら追加していく
while (i < len(left)) and (j < len(right)):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# add the remainging part
if i < len(left):
result.extend(left[i:])
if j < len(right):
result.extend(right[j:])
return result
if __name__ == "__main__":
array = list(map(int, input().split()))
res = merge_sort(array)
print(res)